複利-完全攻略篇

文章參考來源-複利-完全攻略篇

單利

了解複利之前一定得先知道單利是什麼，因為單利與複利之間有著密不可分的關係。複利一定有付息期間，也就是在當期的最後一天，才將利息加到本金上，在期間內所產生的利息均是以單利計算。例如「每月」付息一次的複利，只有在每月的最後一天才以「單利」算出利息，然後再將此利息加上期初的本金，做為下一期計息的本金。這樣的複利也稱作月複利。同樣道理，若每季計息一次，就稱作季複利，意思是當季內產生的利息都是以「單利」計算。

單利的意義：不論付息期間是多久，所茲生的利息均不會加入本金再循環計息，也就是說計息的本金從期初到期末都是一樣的。這樣單利公式就變得很簡單：

設期初本金為 PV，名目利率為 Rn，期間為"t" 年，所以一年會產生的利息金額就是 PV* Rn，再乘上期間"t"，就是單利的公式了：

利息 = PV*Rn*t

期末終值(FV)
= PV + 利息
= PV + PV*Rn*t
= PV*(1+Rn*t) ---------公式(1)

Rn為名目年利率，t 為年數，不足一年以小數或分數表示。例如一季就是(t=1/4)，Rn*t 等於 Rn/4。依此類推一個月(t = 1/12)，一日(t=1/365)，半年(t=1/2)。

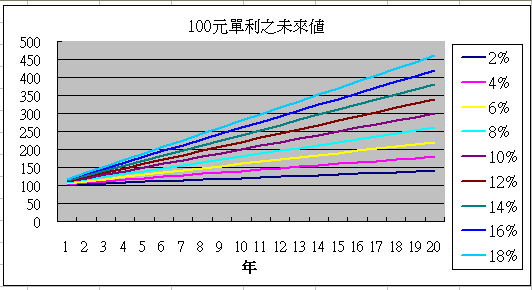
上圖是100元隨著時間(單位：年)以單利成長，可以看出不論時間多長、利率多少，終值或未來值都是以直線上升。

例一：張三跟朋友借款100萬元，約定利息以年利率6%『單利』計算，3年後還款。請問3年後張三必須歸還朋友本金及利息總共多少錢？

本金(PV) = 1,000,000
年利率(Rn) = 6%
年數(t) = 3

期末終值(本利和)= 1000000*(1+6%*3) = 1,180,000

例二：李四跟朋友借款10萬元，約定利息以年利率10%『單利』計算，借款3個月，請問期末李四必須償還朋友多少錢？

本金(PV) = 100,000
年利率(Rn) = 10%
年數(t) = 3/12

期末終值(本利和) =100000*(1+10%*(3/12)) = 102,500

Excel檔案下載

這裡提供一個Excel檔案供讀者下載，裡面共有四張工作表，都是本篇會用到之試算，分別為：

• 單利
• 複利
• 複利次數之影響
• 實質利率

複利

單利的計息方式對貸款者(出借方)似乎不是很公平，因為利息必須等到期末才拿得回來。如果將貸款期間縮短，就可早點拿到利息，這些提早拿回的利息，還可以借給別人生息呢！哈~~~如果世界上只有單利存在的話，那些貸款者將會拼命的將貸款期間縮短，因為那樣對他們會比較有利。

其實比較合理的方式是於借貸期間多了一個『付息期間』，就是每間隔多久結算一次利息。也就是每過一個付息期間，借款者就必須支付貸款者利息。這樣有時候也很麻煩，借款者支付利息非常頻繁，於是就有借款者希望不要每期都支付該筆利息，同意將利息加入本金，做為下期的計息本金。也就是將付息期間一到，變自動將『利息轉貸款』的意思，這就是複利的基本精神。

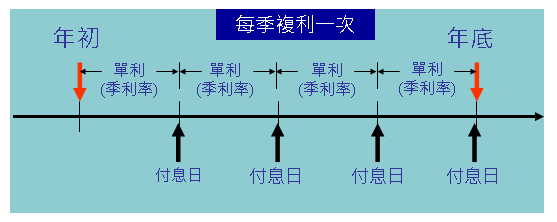
付息期間內以單利計息

付息期間可能是一年、半年、一季或者一個月，甚至於是一個日，全依金融商品而異。付息期間內是以單利計算利息的，只有在付息日才會結算一次利息，然後把利息加入本金當做下一期的本金。例如銀行貸款以及定期存款的付息期間都是一個月，就是一個月結算利息一次，也可以說一個月複利一次的意思。又如債券的付息期間都會載明於債券上面，有每年付息一次的，也有半年付息一次。

複利計算公式

假若本金為PV，每一期之利率為rate，那麼 n 期後之本利和(FV)：

FV = PV*(1+rate)ⁿ ---------公式(2)

這公式的意義是說：每經過一期(付息期間)，就將上期之『期末終值(本利和)』乘上(1+rate)。一開始之期初金額為PV，所以經過 n 期後，期末終值就等於將PV乘上(1+rate)的n次方了。

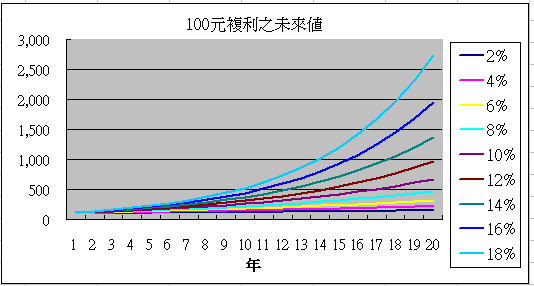
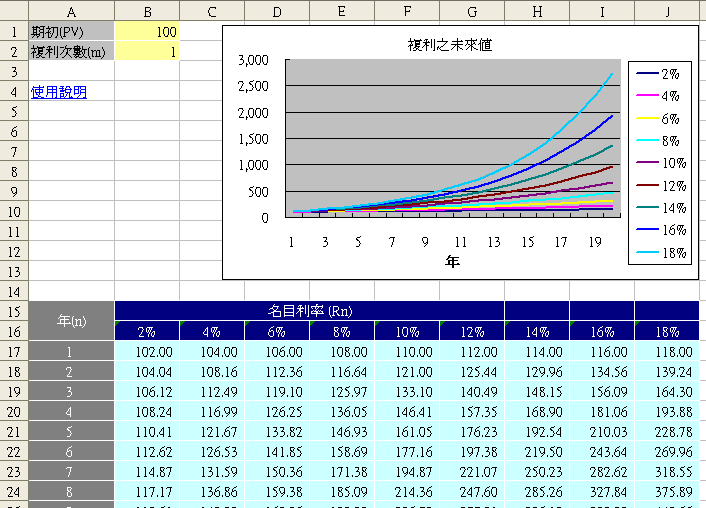
上圖是100元隨著時間(單位：年)以複利成長，可以看出複利終值並非直線，而是以指數成長的，愈到後面成長力道愈大。尤其當利率愈高時，彎度愈大。用數學的語言說：愈到後面，斜率愈大，也就是愈後面每年所成長金額愈大。舉個例子來說：以期初投入100元、2%及18%例，來瞧瞧20年後兩者相差多少？

	2%	18%
1年	102	118
20年	149	2,739

到第一年底時只差了16元，可是20年後可是天壤之別，2%利率只有149元，18%卻有2,739元。

複利公式推導

期末終值(本利和)：
= 期初本金 + 利息
= 期初本金 + 期初本金 *rate
= 期初本金*(1+rate)。

意思是每期末的終值等於該期之期初本金乘上(1+rate)。下表列出1~n期之『期末本利和』之明細，每期之『期末本利和』又當做下一期的『期初本金』去計息。所以第2期之『期初本金』等於第1期之『期末終值』；第3期之『期初本金』等於第2期之『期末終值』，依此類推。可以看出第 n 期之期末終值(FV) = PV*(1+rate)ⁿ。

期數	期初本金	期末終值 (FV)
0		PV
1	PV	PV*(1+rate)
2	PV*(1+rate)	PV*(1+rate)*(1+rate) = PV*(1+rate)2
3	PV*(1+rate)2	PV*(1+rate)2*(1+rate) = PV*(1+rate)3
	....
n	PV*(1+rate)n-1	PV*(1+rate)n

例如：張三跟朋友借款100萬元，約定利息以年利率6%複利計算，3年後還款，每年計息一次。請問3年後張三必須歸還朋友本金及利息總共多少錢？

FV =1000000*(1+6%)³ =1000000*(1+6%)^3 =1,191,016

第1年 = 1000000*(1+ 6%) = 1,060,000
第2年 = 1060000*(1+ 6%) = 1,123,600
第3年 = 1123600*(1+ 6%) = 1,191,016

通用複利公式

公式(2)比較容易令人混淆的是每期利率(rate)及期數(n)。因應付息期間的不同，每期利率及期數算法均有些不同。有無一個通用的式子可以全部都適用呢？例如一般金融機構所都是使用年利率(或稱名目利率 Rn)，名目利率就是去銀行時掛在牆壁上讓大家看的利率表，又名掛牌利率(現在利率變動頻繁，很多銀行現在都改成了LED顯示)。那麼，可以直接使用『名目利率(Rn)』換算成『每期利率(rate)』嗎？

是的，或許那些財務專家們聽到了大家的問題，就另外寫了一個公式，全部以名目利率為基礎。因為付息期間可能是一年、半年或一個月，那麼每期利率就可以用名目利率除上每年計息的次數來換算。每年計息次數一般會以 m 來代表，以半年計息一次為例，等於每年計息2次(m = 2)，也就是說以『半年』為一期，一年有兩期。

每期利率 = Rn / m

可以直接這樣除的原因是：這半年內都以單利計算。依此類推，一月計息一次(m=12)，rate 等於是月利率(Rn / 12)。

期數(n)也得隨著rate的付息期間來改變，例如半年計息一次(m=2)，兩年到期，那麼就得使用半年利率(rate = Rn / m = Rn / 2)。因為一年有兩期，所以兩年就有4期了，所以期數(n)就變成『每年付息次數(m)』乘上『年數(t)』，也就是：n = m*t。

將公式(2)的rate換成(Rn/m)，n換成(m*t)就可寫成通用的複利未來值或終值公式：

FV = PV*(1+Rn/m)^m*t ---------公式(3)

• PV：期初金額
• Rn：名目年利率
• m：每年計息次數(複利次數)
• t：年數

Rn/m的意義是每期的利率，例如Rn / 2 就是半年利率；Rn / 4 就是季利率；Rn / 12 就是月利率。m*t就是總計息次數，也就是俗稱的複利次數，例如每月複利一次(m=12)，3年(t=3)總共複利36次 (12*3)。

例如100元存入銀行，名目年利率6%，每月複利一次，每年12次(m=12)，求3年後之未來值FV？

每月計息一次，就是一年複利12次，所以m = 12。期間為3年(n=3)，所以總共計息次數m*n = 12*3。
FV = 100*(1+6%/12)³⁶
以Excel表示 =100*(1+6%/12)^36 = 119.67

同上例但是改成每季計息一次，求半年之未來值FV？

每季計息一次，就是一年計息4次，所以m = 4。期間為半年(n=1/2)，所以總共計息次數4*(1/2) = 2。
FV = 100*(1+6%/4)²
以Excel表示 =100*(1+6%/4)^2 = 103.02

 

複利次數對未來值之影響

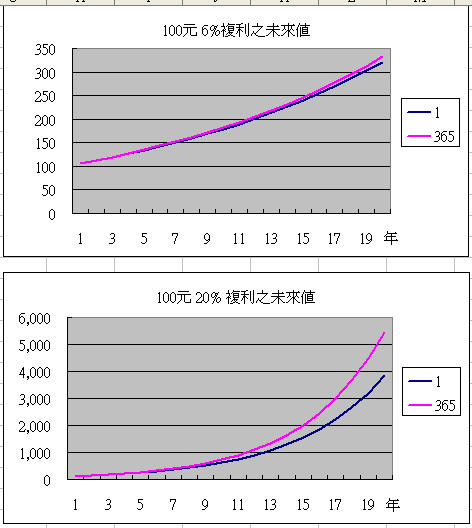
每年複利的次數愈多，實質年利率就愈高，終值就愈高。但是差別到底有多少呢？在下載的Excel檔中，『複利次數之影響』這工作表，期初以100元投入(讀者可自行更改儲存格B1)，分別以名目利率6%、20%兩組，每組均以年複利(1年複利1次)及日複利(1年複利365次)分別計算終值。下面有兩張圖，上圖為6%，下圖為20%。可以看出年利率“6%”的部份，不論每年複利一次或365次，20年之間差別不大。可是再看年利率“20%”(下圖)，這兩者差別可就大了。

所以說利率愈高，每年複利次數的影響愈大。由下圖的分析，可以看出名目利率不大的話，終值對複利次數的敏感度不大。

實質年利率

根據公式(3)，相同本金、相同年利率、相同期間，只是每年的複利次數不一樣時，就會有不同的結果。而且每年複利愈多次，應該得到更多錢才是。沒錯，複利次數愈多，一年後期末未來值就愈高，但不是等比例的提高，而是愈趨近於飽和。以100元存銀行，年利率6%，來看看不同的計息次數結果會有何不同：

計息	Excel公式	未來值	實質年利率
次數		(FV)
1	=100*(1+6%/1)^1	106	6.00%
2	=100*(1+6%/2)^2	106.09	6.09%
4	=100*(1+6%/4)^4	106.14	6.14%
12	=100*(1+6%/12)^12	106.17	6.17%
365	=100*(1+6%/365)^365	106.18	6.18%
∞	=100*EXP(6%)	106.18	6.18%

由上表可以看出計息次數由每年一次到12次時，實質年利率由6.00%升到6.17%，而且愈來愈平。複利次數由12次到365次時，實質年利率卻只由6.17%升到6.18%。也就是說每月複利一次跟每日複利一次沒差多少啦，我想這也是銀行複利次數以月複利為主的原因吧。

連續複利

複利既然那麼厲害，那麼每個貸款者也都心想著：要是能隨時都複利就好了。上表最後一列的每年計息次數就是無窮多次，也就是分分秒秒都在複利的意思，學術界稱這為連續複利。還好~~~上天有眼，沒給那些貸款者太多好處。連續複利實質增加有限，因為從『每月複利』到『每日複利』對實質年利率的改變都不是很大了，那麼『每日複利』到『連續複利』的實質年利率理應也改變不大才是，結果正如所料，還是維持6.18%沒變。

連續複利時，未來值的公式如下：

FV=PV*ｅ^Rn*t

PV是期初值，ｅ是自然指數，Rn 是『名目年利率』，t 是『年』。ｅ在Excel裡用的是EXP函數。

例如100元投資利率6%，以連續複利計，兩年後的終值如下：

FV = 100*e^(6%*2)  以Excel公式表示：

=100*EXP(6%*2)
=112.75

實質年利率公式

實質年利率的意思是：名目利率(Rn)經過一年多次的複利後，相當於一年複利一次的『實質利率』或稱『等值利率』。

利率的意思是：利息佔期初本金的比例，也就是：
利率(Re)
= 利息 / 本金
= (FV - PV) / PV
= FV/PV - 1 ---------公式(4)

FV可用公式(3)去代入，一年複利終值就是當 t = 1，所以將 FV = PV*(1+Rn/m)^m 代入公式(4)

實質利率(Re)：
= PV*(1+Rn/m)^m/ PV -1
=(1+Rn/m)^m- 1 ---------公式(5)

Re =>實質利率 (Effect)，Rn=>名目利率(Nominal )，m =>每年複利次數

一口小台指每月穩定賺取四萬～五萬之關鍵要領提示

文章轉錄出處

我看到很多市場新手，或先前虧損重大者，都在作小台期指。其實無論大台指、小台指下單要領是一樣的，大台指若無要領，作小台指也一樣會賠錢，只是幅度較小而已。
　　『知者行之始；行者知之成』，習取很多學理、方法只是實行的開始，而實現所知所學，才是結果與功效。切勿流於所學無用，一切都是『為用而學』，為何而用？即穩定的賺到錢----不但賺到錢而且穩定，至為重要。
　　期貨波動的過程中，對經驗不俱全者而言，困擾者為始終不知何時切入，切入之後則暴露在行情的波動中，進退之間皆感困惑。那是無法清晰將『行情分解』。對稍有經驗者而言時賺時賠，無法穩定。那是無法將『行情分割』。
　　以下我們以一口小台指每月穩定賺取四萬～五萬為目標，解析完成此一目標的具體關鍵要領：
1.上升趨勢中以K線處理抓取每一波幅段落的回檔結束點，
　過前高後平 倉，也可以隨機獲利。
2.下降趨勢中以K線處理抓取每一波幅段落的反彈結束點，
　破前低後平倉，也可以隨機獲利。
3.短、長均線糾結向上且短趨勢大於長趨勢為起漲，
　可設固定點數平倉獲利。
4.短、長均線糾結向下且短趨勢小於長趨勢為起跌，
　可設固定點數平倉獲利。
5.K線突破群組K線高點時為瞬間上升趨勢成型，
　可設約25~30點平倉。
6.K線跌破群組K線低點時為瞬間下降趨勢成型，
　可設約25~30點平倉。
7.KD指標之有效應用，當長時間波長與短時間波長之KD指標同步進
　入一樣的轉強或轉弱循環時，可以固定點數30~35即平倉獲利。
8.起漲模式出現後，最少會漲升的點數是可以預知的，
　也是可實現的。
9.起跌模式出現後，最少會跌挫的點數是可以預知的，
　也是可實現的。
10.上升趨勢進行中，間或會出現『續漲模式』，也會知其幅度。
11.下降趨勢進行中，間或會出現『續跌模式』，也會知其幅度。
　　以上現象，在每一天的行情中，它都會不斷的重複出現，有時候甚至出現八、九個以上，至少也會出現三、四個。如果我們熟知以上趨勢與循環，每天加以把握三到四個交易，對於完成前述目標，即能順利達成，甚至大幅超越。我不想張大其效益，只願提攜務實達成目標的具體要領與重點。
　　其實；這也就是將行情分解與分割，且我們的資金就根本沒有長時間暴露在市場中。這也是我長時間所累積、所演化的實體經驗。
　　『行遠必自邇；登高必自卑』，萬般財富，緣起於最小，最平實的基本。如果以一口小台指能夠應用要領完成如上目標，進而隨著每個人財富能力的提昇，承受風險能力也相對提高後，逐漸加多交易數量，或二口，以至於一口大台指，二口大台指……。若能如是，則已能實現非但穩定且超乎想像的財富。而切忌操之過急，宜應自我體悟於警惕『貪得者時時貧乏』。關於此；與成就期貨的要領等同重要。
　　特以此鼓勵需要被鼓勵者，幫助需要被幫助者。猶望大家自我提升經驗、智慧與要領層次。

『跳空開高』、『跳空開低』，怎麼對應？

文章轉錄出處

期貨的走勢，由於受美股的連動波動，因此；在開盤時經常有『跳空開高』、『跳空開低』的情形，形成無作價的缺口，在經驗上提供幾個重點，以供有需要者參考應用。
跳空開高：
一、『成交量』注意事項：跳空開高後的第一個五分K線，成交若在3000口以上，應特別注意其低點不能跌破，跌破則易跌難漲。反之；若會續漲，則價位會在該K線的最高價上方波動。
二、『正乖離』注意事項：乖離不是絕對的，而是相對的，因此不能以乖離率為首要判斷條件。在一般情形下，提供幾個數據參考。
（1）對應5分K線之12MA，大於120點以上，視為正乖離太大。
（2）對應3日MA，大於150點以上，視為正乖離太大。
（3）對應5日MA，大於185點以上，視為正乖離太大。
三、『KD值』注意事項：若15KD、30KD、60KD或有任二組KD同步出現開口超過20以上，會止漲修正。
四、『缺口』注意事項：若之前有形成之缺口，則應注意填補缺口後會反向波動。
五、『均線』注意事項：依所設定的均線參數，通常代表時間的挪移與波動，跳空開高後，在前置時間當然皆扣抵低值，要特別注意當時間來到缺口上方時，當下之價位是在其上或其下，以預先判別均線是否即將下彎，或持續上升。
六、『高檔轉折』注意事項：高檔轉折出現的模式有三種，當然如出現高檔轉折與起跌模式，則為上漲趨勢之結束，自然應站在空方。有關於高檔轉折形成之順序，請參閱部內相關文章，茲不擬再贅述。
跳空開低：
一、『成交量』注意事項：跳空開低後的第一個五分K線，成交若在3000口以上，應特別注意其高點是否突破，突破則易漲難跌。反之；若會續跌，則價位會在該K線的最低價下方波動。
二、『負乖離』注意事項：乖離不是絕對的，而是相對的，因此不能以乖離率為首要判斷條件。在一般情形下，提供幾個數據參考。
（1）對應5分K線之12MA，超過120點以上，視為負乖離太大。
（2）對應3日MA，超過150點以上，視為負乖離太大。
（3）對應5日MA，超過185點以上，視為負乖離太大。
三、『KD值』注意事項：若15KD、30KD、60KD或有任二組KD同步出現開口超過20以上，會止跌反彈。
四、『缺口』注意事項：若之前有形成之缺口，則應注意填補缺口後會反向波動。
五、『均線』注意事項：依所設定的均線參數，通常代表時間的挪移與波動，跳空開低後，在前置時間當然皆扣抵高值，要特別注意當時間來到缺口時，當下之價位是在其上或其下，以預先判別均線是否即將上升，或持續下降。
六、『低檔轉折』注意事項：低檔轉折出現的模式有三種，當然如出現低檔轉折與起漲模式，則為下降趨勢之結束，自然應站在多方。有關於低檔轉折形成之順序，請參閱部內相關文章，茲不擬再贅述。
　　我知道很多人常以跳空開高、跳空開低來押注行情，這是不好的動作，總以為押對後會瞬間大幅賺錢，相對的方向錯誤，自然也瞬間大幅虧錢。善勸大家勿以這樣的心態與動作進行操作。
　　留倉與否，其實亦有其要領，如美股出現起跌或續跌模式，則利用其反彈後留空單。反之；如美股出現起漲或續漲模式，則利用其回檔後留多單。關於此；不擬於此詳述。

不瞭解這些關鍵重點，即無法扭轉賠錢的慣性

文章轉錄出處

幾乎所有的參與交易的人，都窮盡一切之力量、傾其所有之努力在找尋如何穩定獲利的要領與方法。惟成功者終歸是極少數。
　　股票期貨的學理、方法太多，旁門左道更多，究竟要擁有多少經驗？成就什麼方法才能賺到錢？其實有其關鍵重點、關鍵方向與關鍵要領。
　　以下提出幾個關鍵重點予有需要者參考，並自發深省，從而探究其答案即能扭轉賠錢的慣性，並實現穩定獲利之效益。
（一）能夠很明確分辨多方趨勢，並知道在多方趨勢裡，養成不要有放空的
　　　想法與動作，直到慣性改變，趨勢結束。
（二）多方趨勢裡，既不要放空，主要係以回檔買進為主。問題是回檔至何
　　　處？回檔結束點已然有要領處理。
（三）能夠很明確分辨空方趨勢，並知道在空方趨勢裡，養成不要有作多的
　　　想法與動作，直到慣性改變，趨勢結束。
（四）空方趨勢裡，既不要作多，主要係以反彈放空為主。問題是反彈至何
　　　處？反彈結束點已然有要領處理。
（五）為及時與有效掌握趨勢，對不同時間波長的均線參數設置，都能力求
　　　不過於敏感與不過於遲鈍。
（六）在多方趨勢中，如何放任漲勢以擴大利潤，並在漲勢進行中，每一個
　　　時刻當下，由於始終知道關鍵價位，而知所進退。
（七）在空方趨勢中，如何放任跌勢以擴大利潤，並在跌勢進行中，每一個
　　　時刻當下，由於始終知道關鍵價位，而知所進退。
（八）當上漲趨勢形成時，每一時刻所變化足以影響上漲慣性存續與消失的
　　　關鍵點位，始終知道?
（九）當下跌趨勢形成時，每一時刻所變化足以影響下跌慣性存續與消失的
　　　關鍵點位，始終知道?
（十）熟悉『起漲模式』，因為它是空方趨勢結束的剎那亦為多方趨勢開始
　　　的剎那。
（十一）熟悉『起跌模式』，因為它是多方趨勢結束的剎那亦為空方趨勢開
　　　　始的剎那。
（十二）熟悉上升趨勢中之『續漲模式』。
（十三）熟悉下降趨勢中之『續跌模式』。
（十四）明確知道『低檔轉折』之成型與演化順序。
（十五）明確知道『高檔轉折』之成型與演化順序。
（十六）在均線上升過程，股價波動至均線附近固為買點，但有兩個關　
　　　　鍵成敗重點：
　　　　　　　①均線參數要妥當
　　　　　　　②股價來到均線附近的時空變化，均線扣抵位置
　　　　　　　　是在其下方。
（十七）在均線下降過程，股價波動至均線附近固為賣點，但有兩個關
　　　　鍵成敗重點：
　　　　　　　①均線參數要妥當
　　　　　　　②股價來到均線附近的時空變化，均線扣抵位置是
　　　　　　　　在其上方。

      說穿了；將以上這些問題加以整合、串連亦即為行情波動的分解，這是關鍵重點，也是買賣成敗的關鍵因素。
　　能夠這樣；就不會錯把買點當賣點、錯把賣點當買點，買賣點才不會錯置。也終於能扭轉賠錢的慣性，並進而開始能夠獲利並且穩定。

在空方趨勢頻頻作多的人，在多方趨勢必然會不斷放空

文章轉錄出處

由於投資人在金融市場，並無法像皮膚有感應寒暑的本能，
天冷了自然穿衣禦寒，又如「春耕」、「夏耘」、「秋收」、
「冬藏」，不會做錯動作，但是在金融市場則完全不然，
不斷的做錯動作。
　　什麼是對的動作？當進入空方時空循環時，
一則渾然不知，二則看股價下跌，只要是人性，都以為便宜以為
是機會，就會不斷買進，甚至所謂搶反彈，但有經驗者皆知，
　　在空方循環只有一個動作，就是「反彈賣出」，其他動作都是錯的。
反之，在多方循環時也只有一個動作，就是「回檔買進」，
直到趨勢反轉。但一般投資人都以為股價漲高了，而趕快賣出。
　　在多方趨勢裡，由於股價不斷上漲，遇到這樣的時空背景，
有兩種人產生了兩種思維模式與行為模式：
第一種人是越漲越空。
第二種人是謹慎小心，不敢買進，深怕套牢但其實漲也不敢買，
跌也不敢買，經過觀望、等待、小心、謹慎，最後按耐不住買進時，
通常已是相對高檔，一經價格波動，就不知方向，進退兩難。
這是在多方趨勢中輸家的的思維方式與行為模式。反之; 贏家的思維
與行為模式是利用拉回買進，即漲勢中的跌勢買進。當然回檔會有
多深，以何要領對應，恕難與此公開揭露。
　　在空方趨勢裡，由於股價不斷下跌，遇到這樣的時空背景，
有兩種人產生了兩種思維模式與行為模式：
第一種人是越跌越買。
第二種人是謹慎小心，不敢放空，深怕賠錢但其實跌也不敢賣，
漲也不敢賣，經過觀望、等待、小心、謹慎，最後按耐不住放空時，
通常已是相對低檔，一經價格波動，就不知方向，進退兩難。
這是在空方趨勢中輸家的的思維方式與行為模式。反之; 贏家的思維
與行為模式是利用反彈放空，即跌勢中的漲勢賣出或放空。
當然反彈會有多大，以何要領對應，恕難與此公開揭露。
　　期貨市場下單的是人，由於人的不完美與無經驗，因之會產生很多
障礙，沒有累積足夠之經驗，獲得周全之要領前，通常會犯了只要
是人就會不自覺犯下主觀與判斷上的差錯，這也就是，95%為輸家的
原因。
　　因此期勉大家，要不斷提昇自己的經驗與要領層次。在經驗不俱足、
要領不周全前，應自我警惕戒慎，少量下單為要。

由五日均量與十日均量之交相變化，看股價在作什麼？

文章轉錄出處

『價』是『價』造就的。若不是由量造就的價格，將無以持續，也很快會改變。我們對於漲漲跌跌的股價變化，重視其趨勢；那麼，量的增增減減自然亦有其趨勢，因此也必須重視它的趨勢變化。
　　量除重視成交量，也必須重視均量，成交量對應均量產生的趨勢變化，大抵如同價格對應均價所產生的趨勢變化。
　　茲以五日均量與十日均量為例，由其交相變化判斷股價的時空位置，亦即股價在作什麼？
1/五日均量↑，十日均量↑而且五日均量大於十日均量。為漲升結構。
2/五日均量↓，十日均量↑而且五日均量大於十日均量。為漲多修正。
3/五日均量↓，十日均量↑而且五日均量小於十日均量。為回檔結構。
4/五日均量↓，十日均量↓而且五日均量小於十日均量。為跌挫結構。
5/五日均量↑，十日均量↓而且五日均量小於十日均量。為跌多修正。
6/五日均量↑，十日均量↓而且五日均量大於十日均量。為反彈結構。
　　以上提供有需要者參考，並據以舉一而反三加以活用，將量的趨勢與價的趨勢合併運用，會更臻完美，更具勝機。當然五日均量可改為任何之五均量，十日均量可改為任何之十均量，其要領是一樣的。
　　此外；在注意量的變化之時，異常大量不能忽略。須知異常大量後股價會有異常的變化，異常變化有兩種：其一向上異常波動，其二向下異常波動。
　　異常大量實為較大資金部位之瞬間進場或分段進場的現象。經驗上究竟多大量才認定異常大量？如何判別其為進貨？抑或出貨？他日有機會另文再談。
　　以上純以量與均量變動的觀點提供量亦有其趨勢，要加以格外重視。又金融市場無絕對，我們要掌握的是常態波動下『相對的絕對』。
　　如果你認同我的看法，那麼請多加活用與運用。